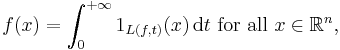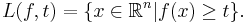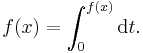Layer cake representation

In mathematics, the layer cake representation of a non-negative, real-valued measurable function f defined on n-dimensional Euclidean space Rⁿ is the formula

$f(x) = \int_{0}^{%2B \infty} 1_{L(f, t)} (x) \, \mathrm{d} t \mbox{ for all } x \in \mathbb{R}^{n},$

where 1_E denotes the indicator function of a subset E ⊆ Rⁿ and L(f, t) denotes the super-level set

$L(f, t) = \{ x \in \mathbb{R}^{n} | f(x) \geq t \}.$

The layer cake representation follows easily from the formula

$f(x) = \int_{0}^{f(x)} \mathrm{d} t.$

The layer cake representation takes its name from the representation of the value f(x) as the sum of contributions from the "layers" L(f, t): "layers"/values t below f(x) contribute to the integral, while values t above f(x) do not.

References

Gardner, Richard J. (2002). "The Brunn-Minkowski inequality". Bull. Amer. Math. Soc. (N.S.) 39 (3): 355–405 (electronic). doi:10.1090/S0273-0979-02-00941-2.
Lieb, Elliott H., & Loss, Michael (2001). Analysis (Second ed.). Providence, RI: American Mathematical Society. ISBN 0-8218-2783-9.